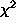 test is performed with each member of the expected
array equal to the number of random fractions divided by 10.
test is performed with each member of the expected
array equal to the number of random fractions divided by 10.
We also wrote two variations of this test. The first one groups the random numbers into pairs, the second one into triples. The expected values of each pair and triple are then the number of random fractions divided by 2*100 and by 3*125 (5 intervals) respectively.
- 1 - All of the same or two different integers in a group.
- 2 - Three different integers in a group.
- 3 - Four different integers in a group.
- 4 - Five different integers in a group.
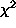 test is performed with the following expected values for each category (n is the number of fractions):
test is performed with the following expected values for each category (n is the number of fractions):
- 1 - 0.0136 n.
- 2 - 0.1800 n.
- 3 - 0.5040 n.
- 4 - 0.3024 n.
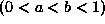 .
Each random number is replaced with 0 if outside and with 1 if inside
the interval. We are interested in the lengths of the gaps.
The expected value of a gap of length k is :
.
Each random number is replaced with 0 if outside and with 1 if inside
the interval. We are interested in the lengths of the gaps.
The expected value of a gap of length k is :

- 1 - sequence of 5.
- 2 - sequence of 6.
- ..
- 15 - sequence of 19.
- 16 - sequence of 20 or more.
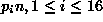
with n the number of fractions and  from the following sequence
of probabilities :
0.03840000, 0.07680000, 0.09984000, 0.10752000, 0.10450944, 0.09547776, 0.083816
45, 0.07163904, 0.06011299, 0.04979157, 0.04086200, 0.03331007, 0.02702163, 0.02
184196, 0.01760857, 0.07144851
from the following sequence
of probabilities :
0.03840000, 0.07680000, 0.09984000, 0.10752000, 0.10450944, 0.09547776, 0.083816
45, 0.07163904, 0.06011299, 0.04979157, 0.04086200, 0.03331007, 0.02702163, 0.02
184196, 0.01760857, 0.07144851




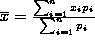 test with the observed values with the method from the
analysis class.
The hypothesis of randomness is rejected if the probability is less then
0.05 (no randomness) or more then 0.95 (fabricated) in 95% or more of the experiments.
test with the observed values with the method from the
analysis class.
The hypothesis of randomness is rejected if the probability is less then
0.05 (no randomness) or more then 0.95 (fabricated) in 95% or more of the experiments.